Berechnung feuchter Luft

Trockene Luft besteht zu ca. 78 % aus Stickstoff, 21 % Sauerstoff und 1 % aus Argon. Abhängig von den Umgebungsbedingungen kann dieses Gasgemisch Wasserdampf aufnehmen, in unseren Breiten sind es im Mittel ca. 1,3 %. Überschreitet der Wasserdampfgehalt einen temperaturabhängigen Höchstwert, dann kommt es zur Kondensation. Man spricht von einer Sättigung der Luft. Die dann in einem Volumen enthaltene Wassermenge wird als Sättigungsfeuchte bezeichnet und in g Wasser je kg trockener Luft angegeben.

Der Ausdruck „Wasseraufnahme“ suggeriert, dass der Wasserdampf in irgendeiner Form in der Luft gelöst ist oder von ihr getragen wird, was aber nicht der Fall ist. Wasser- und Luftmoleküle bewegen sich unabhängig voneinander im selben Volumen. Nach dem Gesetz von Avogadro hängt die Zahl der Moleküle in einem Gasvolumen nur von Druck und Temperatur ab. Die Wasserdampfmoleküle verdrängen daher einen gewissen Teil der Luftmoleküle. Da das Molekulargewicht von Wasser nur ca. 62 % des Luftgewichtes beträgt, nimmt die Dichte der Mischung mit steigendem Dampfgehalt geringfügig ab, die spezifische Wärmekapazität von Wasserdampf ist dagegen höher (cp_Luft = 1,006 kJ/kgK, cp_Dampf = 1,86 kJ/kgK), so dass die Wärmekapazität des Gemisches ansteigt.

Die Gasanteile der feuchten Luft beeinflussen sich gegenseitig in Ihrem Verhalten kaum. Insbesondere hängt die Kondensation des Wassers praktisch nicht vom Luftdruck ab, sondern nur vom Partialdruck des Dampfes. Die Sättigungsdampfmenge ist also (nahezu) unabhängig davon, ob sich im Raum Luft befindet oder nicht. Der Dampfdruck, der sich bei Sättigung in einem luftleeren Raum einstellen würde, wird als Sättigungspartialdruck bezeichnet.

Die Ursache für dieses Verhalten liegt darin, dass die Kondensation durch die starken Bindungskräfte zwischen den Wassermolekülen entsteht. Trifft ein Wasser- auf ein Luftmolekül, dann wirken nur schwache molekulare Kräfte. Treffen zwei Wassermoleküle aufein­ander, dann haben sie die Neigung zu agglomerieren. Befinden sich sehr viele Wassermoleküle in einem Volumen, dann kommt es häufig zu solchen Zusammenstößen, so dass schließlich ein Teil der Moleküle zu Wassertropfen kondensieren kann. Steigt die Temperatur, dann steigt auch die Bewegungsenergie der Wassermoleküle, so dass diese vermehrt aus den Tropfen herausgeschleudert werden und wieder in die Dampfphase eintreten. Zwischen Wasser und Dampf bildet sich ein Gleichgewichtszustand, der stark temperaturabhängig ist.

Das Mollier h,x-Diagramm

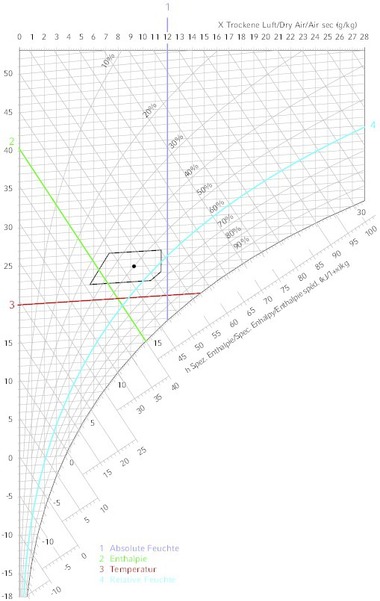
Vier Zustandsgrößen der feuchten Luft sind im Mollier h,x-Diagramm (Bild 1) zusammengefasst:

h Enthalpie in [kJ/kg trockene Luft]

t Temperatur in [°C]

x Absolute Feuchte in [g/kg trockene Luft]

phi relative Feuchte in [%]

Die Enthalpie-Linien des Diagramms laufen nicht – wie der Name erwarten lässt – horizontal, sondern schräg zur Abszisse. Lediglich die Temperaturlinie für 0 °C läuft exakt horizontal, alle anderen Temperaturlinien spreizen sich aufgrund der steigenden spezifischen Wärmekapazität des Gemisches mit steigenden Dampfgehalten auf und verlaufen somit unter einem leichten Winkel zur Horizontalen.

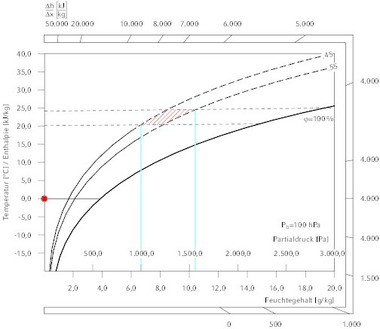
Produktiv eingesetzte h,x-Diagramme enthalten häufig noch diverse Zusatzinformationen. So kann zusätzlich die Gasdichte im Diagramm eingetragen sein oder es findet sich ein Randmaßstab, mit dem sich Zustandsänderungen über ihren Winkel mit einem Maßstab ∆h/∆x abgreifen lassen. Sie sind damit ein wertvolles Hilfsmittel zur Beschreibung und Dimensionierung von komplexen klimatechnischen Systemen.

Die Grenzen gedruckter Diagramme zeigen sich allerdings, wenn die Luftdrücke in einem Prozess wesentlich von den Standardbedingungen (1013 hPa) abweichen oder sich Temperaturen oberhalb von 50 °C und Feuchten über 30 g/kg einstellen. An dieser Stelle kann der im Folgenden vorgestellte Funktionssatz weiterhelfen, der für Temperaturen bis 90 °C und absolute Feuchten bis 150 g/kg einsetzbar ist. Die Daten wurden mit den in der DIN 4108 angegebenen bauphysikalischen Werten sowie Tabellenwerten nach Glück [1] verglichen. Die Abweichungen der Stoffwerte liegen im Bereich von 0 °C bis 60 °C unter 0,1 % (Dichteabweichung < 0,25 %), bei 90 % werden in allen Werten 0,65 % nicht überschritten.

Schnellkurs in VBA

Der vorgestellte Funktionssatz wurde als Erweiterung für Microsoft Excel entwickelt und nutzt die eingebaute Programmierschnittstelle Visual Basic for Applications (Die Funktionen wurden unter der Version 2000 und 2003 geschrieben, sind aber auch unter neueren Versionen lauffähig). Viele Anwender scheuen hier den Einstieg („Ich bin doch kein Programmierer…“), was aber zumindest auf der Ebene der Funktionsprogrammierung unbegründet ist. Diese ist in Excel-VBA so einfach gestaltet, dass der Einsatz unkompliziert und häufig lohnend ist.

Zu Erstellung neuer Funktionen für Excel muss zunächst der VBA-Editor geöffnet werden (Excel Alt-F11)¹. Im Projektexplorer fügt man nun an die aktuelle Arbeitsmappe mit der rechten Maustaste -> Einfügen -> Modul ein neues Programmmodul an und schon kann die Programmierung beginnen.

Neue Funktion können einfach wie folgt erzeugt werden:

Function Test(x, y)

Test = x ^ 2 + y     ‘ Dies ist ein Kommentar

End Function

Die so definierte Funktion kann direkt nach der Eingabe bereits in Excel-Arbeitsblättern genutzt werden. Sie findet sich im Funktionsassistenten unter der Kategorie „Benutzerdefiniert“ und kann wie jede andere Funktion in Excel verwendet werden. In der Grundeinstellung müssen im VBA Variablen nicht vereinbart werden. Sie können dann beliebige Werte enthalten, also Zahlen, Texte oder sonstiges, da sie vom Typ Variant sind. Es ist allerdings vorteilhaft, grundsätzlich Variablentypen zu vereinbaren, da hierdurch die Berechnung wesentlich schneller ausgeführt werden kann. Bei Variablen geschieht dies mit der Anweisung „Dim Variable As Typ“. Als Typ wird häufig Double (Fließkomma) und Integer verwendet.

Function Test(x as Double, y as Integer) as Double

Dim A As Double

A = x ^ 2 

Test = A * y     ‘ Nur ein Beispiel

End Function

Anstelle der Definition mit „As“ lassen sich auch Kurzzeichen direkt hinter dem Namen verwenden, und zwar % für integer und # für Double. Beide Formen lassen sich auch mischen. Das obige Beispiel könnte dann so aussehen:

Function Test(x#, y%) As Double

Dim A#

A = x ^ 2 

Test = A * y     ‘ Nur ein Beispiel

End Function

Sofern man sich auf der Ebene der Funktionsprogrammierung bewegt, ist damit das notwendige Wissen schon fast erschöpft, so dass wir uns nun der Feuchteberechung zuwenden können.

Funktionssatz für die Berechnung feuchter Luft

Der im Folgenden beschriebenen Funktionssatz ist orthogonal, d.h. er erlaubt eine Umrechnung aller vier Zustandsgrößen aus jeweils zwei anderen, und zwar in allen denkbaren Kombinationen. Als Namenskonvention beginnen alle Funktionen mit dem Buchstaben F gefolgt von der berechneten Zustandsgröße. Dann folgen, getrennt durch einen Unterstrich, die Eingangsgrößen. Fx_t_phi( ) bedeutet also, dass hier x aus t und phi berechnet wird.

Folgende Funktionen wurden implementiert:

// Hilfgrößen

Function RhoLuft(T, x, Optional patm = Nulldruck) 

Function CPLuft(x)

Function FPS_t(t)    

Function Ft_PS(ps)   

Function Fpp_x(x, Optional patm = Nulldruck)

Function Fx_pp(Partialdruck, Optional patm = Nulldruck)

// Zustandsgrößen

Function Fx_t_phi(t, Optional phi = 1, Optional patm = Nulldruck)

Function Fx_t_h(t, h) 

Function Fx_h_phi(h, Optional phi = 1, Optional patm = Nulldruck)

Function Fphi_t_x(t, x, Optional patm = Nulldruck)

Function Fphi_t_h(t, h, Optional patm = Nulldruck)

Function Fphi_x_h(x, h, Optional patm = Nulldruck)

Function Ft_x_phi(x, Optional phi = 1, Optional patm = Nulldruck)

Function Ft_x_h(x, h) 

Function Ft_h_phi(h, Optional phi = 1, Optional patm = Nulldruck)

Function Fh_t_x(t, x) 

Function Fh_t_phi(t, Optional phi = 1, Optional patm = Nulldruck)

Function Fh_x_phi(x, Optional phi = 1, Optional patm = Nulldruck)

// Hilfsfunktionen für die Darstellung von Diagrammen

Function FY_t_x(t, x)

Function Ft_x_y(x, y)

„Optional“ bedeutet, dass dieser Parameter weggelassen werden kann und durch den Vorgabewert ersetzt wird. Bei allen Funktionen ist dies der Atmosphärendruck, für den dann 101300 Pa eingesetzt werden. Wird die relative Feuchte nicht angegeben, dann werden die Werte an der Sättigungslinie berechnet (phi = 100 %). Bei allen Funktionen gelten folgende Konventionen:

t = Temperatur in [°C]

p = Druck in [Pa]

pp = Partialdruck [Pa ]

ps = Sättigungspartialdruck [Pa]

h = Enthalpie in [kJ/kg]

m = Massenstrom [kg/s]

phi = relative Feuchte in [0..1]

x = Absolute Feuchte [g Wasser/kg trockene Luft]

Die verwendeten Konstanten sind:

Const Nulldruck = 101 300 ’ Pa

Const cpl = 1.006 ’ Spezifische Wärmekapazität Luft in kJ/kg

Const cpd = 1.86 ’ Spezifische Wärmekapazität Dampf in kJ/kg

Const r0 = 2501.6 ’ Verdunstungswärme des Wassers bei 0 °C in kJ/kg

Const RL = 287.055 ’ Gaskonstante Luft

Const RD = 461.51 ’ Gaskonstante Dampf

Const E0 = 610.5695397 ’ Bezugsdruck der Magnus-Formel in hPa

Const K1 = 17.177 ’ °C

Const K2 = 235.77 ’ °C

Const K3 = 22.52447 ’ °C

Const K4 = 273.15 ’ °C

Const K5 = 0.998064758 ’ Korrekturfaktor

Const K6 = 622.2 ’ Verhältnis RLuft / RDampf * 1000

Basisfunktionen Dichte, spezifische Wärmekapazität und Dampf­druck

Zunächst werden einige allgemeine Funktionen implementiert. Insbesondere die spezifische Wärmekapazität der feuchten Luft wird bei der Enthalpieberechnung benötigt. Die Dichte der feuchten Luft ergibt sich aus der allgemeinen Zustandsgleichung als ρ = p / (R x T), wobei R die Gaskonstante des Gemisches ist. Diese ergibt sich aus der Mittelung der Gaskonstanten von Dampf und Luft entsprechend der Massenanteile.

Für beide Funktionen wird der gewichtete Mittelwert entsprechend den Massenanteilen von Luft und Dampf benötigt. Die absolute Feuchte x ist aber nicht der Massenanteil des Gemisches, sondern sie ist bezogen auf die Trockenluftmasse. Daher wird zunächst eine Gewichtungsfunktion benötigt, die dieser Definition gerecht wird

’ Gewichtetes Mittel abhängig von x

Function GewMittel (x#, WL, WD) As Double

Dim xt#

xt = x / 1000

GewMittel = (WL + xt * WD) / (1 + xt)

End Function

’ Dichte der Luft

Function RhoLuft (t#, Optional x# = 0, Optional patm# = Nulldruck) As Double

RhoLuft = patm / ((t + 273) * GewMittel (x, RL, RD))

End Function

’ Wärmekapazität feuchter Luft

Function CPLuft (x#) As Double

CPLuft = GewMittel (x, cpl, cpd)

End Function

Der Sättigungspartialdruck ist die entscheidende Basisgröße der Feuchteberechnung. Hier wird die so genannte Magnus-Formel verwendet. Die Konstante K1 bis K5 wurden leicht modifiziert, um eine bessere Übereinstimmung der Daten im oberen Temperaturbereich zu erhalten. Für Temperaturen unter 0 °C werden aufgrund der Eisbildung andere Konstanten verwendet als bei höheren Temperaturen.

Es ist zu beachten, dass in VBA Exp(x) die Schreibweise für e^x ist, Log(x) der natürliche Logarithmus. Der Vollständigkeit halber wurde die Umkehrfunktion mit angegeben.

’ Sättigungsdampfdruck genauer als 0.1 %, 0-90 °C

Function FPS_t(ByVAL t#) As Double

Dim z#

If t >= 0 Then

z = K1 * t / (K2 + t)

Else

z = K3 * t / (K4 + K5 * t)

End if

FPS_t = E0 * Exp (z)

End Function

’ Umkehrung t aus PS

Function Ft_PS(ps#) As Double

Dim w#

w = Log (ps / E0)

If ps > E0 Then

Ft_PS = K2 / (K1 / w – 1)

Else

Ft_PS = K4 / (K3 / w – K5)

End if

End Function

Der Partialdruck des Wasserdampfes kann über das Verhältnis der Gaskonstanten K6 leicht aus der absoluten Feuchte berechnet werden, hier ebenfalls mit Umkehrfunktion.

’ Fpp_x Partialdruck aus x berechnen

Function Fpp_x(x#, Optional patm# = Nulldruck) As Double

If x <= 0 Then

Fpp_x = 0

Else

Fpp_x = patm / (K6 / x + 1)

End If

End Function

’ Fx_pp as Absolute Feuchte aus dem Partialdruck berechnen

Function Fx_pp (Partialdruck#, Optional patm# = Nulldruck) As Double

If Partialdruck <= 0 Then

Fx_pp = 0

Else

Fx_pp = K6 / (patm / Partialdruck – 1)

End if

End Function

Nun sind die Vorarbeiten abgeschlossen und die Funktionen für die Zustandsgrößen können implementiert werden.

Berechnungsfunktionen für die Zustandsgrößen x, t, h und phi

Die implementierten Funktionen wurden oben als sortierte Liste angegeben. Im Folgenden werden die Einzelberechnungen entsprechend Ihrer logischen Abhängigkeit dargestellt.

Einige Größen können direkt aus den Stoffwerten berechnet werden. So ergibt sich die Enthalpie aus der spezifischen Wärmekapazität der Einzelstoffe zuzüglich der Verdunstungsenthalpie des Wassers. Aufgrund der Definition von der absoluten Feuchte bezogen auf den Trockenluftanteil addiert sich die Wasserdampfenthalpie einfach zu Luftenthalpie.

’ Enthalpie feuchter Luft

Function Fh_t_x(t, x#) As Double

Fh_t_x = cpl * t + (cpd * t+ r0) * x / 1000

End Function

’ Absolute Feuchte aus t und h

Function Fx_t_h(t, h#) As Double

Fx_t_h = (h – cpl * t) / (cpd * t + r0) * 1000

End Function

’ Temperatur aus x und h

Function Ft_x_h(x#, h#) As Double

Ft_x_h = (h – r0 * x / 1000) / CPLuft(x)

End Function

Die Umrechnungen zwischen t, x und h sind aufgrund der linearen Abhängigkeiten einfach, bei der Berechnung der Temperatur aus x und h wird auf die bereits implementierte Funktion zu Berechnung der spezifischen Wärmekapazität zurückgegriffen.

Berechnungen auf Basis von Partialdruck und Sättigungs­partial­druck

Die relative Feuchte lässt sich aus dem Verhältnis von aktuellem Partialdruck zum Sättigungspartialdruck berechnen. Da oben bereits die Funktionen für den Partialdruck bei gegebener absoluter Feuchte (Fpp_x) sowie deren Umkehrung implementiert wurden, sind die Berechnungen einfach.

Für x aus t und Phi wird zunächst der Sättigungsdampfdruck bei der Temperatur d berechnet. Der Partialdruck pp ist dann ps*phi. Fx_pp berechnet daraus die absolute Feuchte.

Die relative Feuchte aus t und x berechnet sich aus dem Verhältnis von Sättigungspartialdruck bei der Temperatur t und dem Partialdruck bei der Feuchte x.

Sind Phi und x gegeben, dann kann aus diesen Größen der Sättigungspartialdruck berechnet werden. Diesem lässt sich dann eine Sättigungstemperatur zuordnen (Die angegebenen Funktionen enthalten der Übersichtlichkeit halber keine Fehlerprüfung.

Bei Phi = 0 würde hier also ein DivisionByZero-Fehler auftreten, der abgefangen werden solle, z. B. durch voranstellen einer Zeile If phi <= 0 Then Exit Function. Das Ergebnis der Funktion ist dann immer 0).

’ x aus t und phi berechnen, t in °C, phi in 0…1, x in g/kg

Function Fx_t_phi(#, Optional phi# = 1, Optional patm# = Nulldruck) As Double

Fx_t_phi = Fx_pp(FPS_t(t) * phi, patm)

End Function

’ phi aus x und t berechnen

Function Fphi_t_x(t, ByVal x#, Optional patm# = Nulldruck) As Double

Fphi_t_x = Fpp_x(x, patm) / FBS_t(t)

End Function

’ Temperatur aus x und phi berechnen

Function Ft_x_phi(x#, Optional phi# = 1, Optional patm# = Nulldruck) As Double

Dim ps#

Ps = Fpp_x(x, patm) / phi

Ft_x_phi = Ft_PS(ps)

End Function

Abgeleitete Funktionen

Aus den bisher implementierten Funktionen lassen sich nahezu alle weiteren Größen durch Kombination ableiten. So kann phi aus t und h indirekt berechnet werden, indem man zunächst das x mit Fx_t_h berechnet und dann Fphi_t_x nutzt (Formelkasten 7). Analog lässt sich Fphi_x_h, Fh_t_phi und Fh_x_phi darstellen.

’ rel Feuchte aus t und h berechnen

Function Fphi_t_h(t, h#, Optional patm# = Nulldruck) As Double

Fphi_t_h = Fphi_t_x(Ft_x_h(x, h), x)

End Function

’ rel Feuchte aus x und h berechnen

Function Fphi_x_h(x#, h#, Optional patm# = Nulldruck) As Double

Fphi_x_h = Fphi_t_x(Ft_x_h(x, h), x)

End Function

’ Enthalpie berechnen aus Temperatur und rel Feuchte

Function Fh_t_phi(ByVal t#, Optional phi# = 1, Optional patm# = Nulldruck) As Double

Fh_t_phi = Fh_t_x(t, Fx_t_phi (t, phi, patm)

End Function

’ Enthalpie berechnen aus Absoluter und rel Feuchte

Function Fh_x_phi(x#, Optional phi# = 1, Optional patm# = Nulldruck) As Double

Fh_x_phi = Fh_t_x(Ft_x_phi (x, phi, patm), x)

End Function

Mit den bis hier vorgestellten Funktionen lassen sich zehn der zwölf angegebenen Umrechnungen ausführen. Es fehlen noch zwei Berechnungen, die Werte aus einer Kombination von h und phi berechnen.

Berechnungen aus h und phi

Da die Temperatur und absolute Feuchte bei Rechnungen mit h und phi als Ausgangsgrößen unbekannt sind kann der Zustandsgröße phi kein eindeutiger Wert zugeordnet werden. Als natürlicher Ansatz zur Lösung muss daher der Schnittpunkt der h- und phi-Linie iterativ ermittelt werden. Aufgrund der geringen und stetigen Krümmung der phi-Linien eignet sich ein modifiziertes Newton-Verfahren sehr gut für die Berechnung (Bild 2).

Als Startwerte wird zunächst die Enthalpie auf der phi-Linie für zwei frei gewählte Temperaturen (hier 20 °C und 30 °C) berechnet. Über eine lineare Interpolation wird der Schnittpunkt der Verbindungslinie dieser beiden Werte mit der h-Linie berechnet. Dieser liegt typischerweise sehr nah an der gesuchten Zieltemperatur. Ein zweiter Näherungswert wird in der Nähe dieser Temperatur auf Basis der verbleibenden Enthalpiedifferenz abgeschätzt. Beide Punkte liegen so nah am Zielwert, dass bereits im nächsten Iterationsschritt häufig eine Genauigkeit der Temperatur von 10 ^-3K erreicht wird.

Aufgrund der gewählten Startwerte konvertiert das Verfahren im Bereich zwischen 10 bis 40 °C besonders schnell, im Bereich von -10 bis 60 °C werden nicht mehr als drei Iterationen benötigt. Diese schnelle Konvergenz ist wichtig, da in jedem Iterationsschritt zweimal die Funktion Fh_t_phi() aufgerufen wird, deren Berechnung vergleichsweise langsam erfolgt. 

’ Enthalpie berechnen aus Temperatur und rel Feuchte

Function Ft_h_phi(h#, Optional phi# = 1, Optional patm# = Nulldruck) As Double

Dim t#, t1#, t2#, h1#, h2#, ht#, DH#

t1 = 20 ’ 1. Schätzwert 20 °C

h1 = h – Fh_t_phi(t1, phi) ’ h-Abstand zur rel Feuchtelinie

t2 = t1 + 10 ’ 2. Schätzwert 30 °C

Do ’ Schleife <------------------------

h2 = h – Fh_t_phi(t2, phi) ’ 2. h-Abstand zur rel Feuchtelinie DH = h1 – h2 ’ Neues t berechnen nach Newton

t = t1 + (t2 – t1) * h1 / DH ’ t und hat schon nah am Ziel ht = h – Fh_t_phi(t, phi) ’

If Abs(hat) >= 0.01 Then ’ Neue Schätzwerte berechnen

t2 = t + 0.5 * (t2 – t) * (ht) / Abs(h1 – h2)

’ Rechts abschätzen aus vorh. Schritt

t1 = t ’ Startwert links ist t

h1 = ht ’ Die Differenz für h1 schon bekannt

End If

Loop Until Abs(ht) <= 0.01 ‘ Schleife bei dt > 0.01----------------

Ft_h_phi = t

End Function

Auf Basis der beschriebenen iterativen Funktion kann nun noch die letzte Funktion Fx_h_phi implementiert werden, so dass alle zwölf Umrechnungen möglich sind. Damit lässt sich jede Zustandsgröße aus zwei anderen berechnen.

Function Fx_h_phi(h#, Optional phi# = 1, Optional patm# = Nulldruck) As Double

Fx_h_phi = Fx_t_phi(Ft_h_phi (h, phi), phi)

End Function

Y, die fünfte Zustandsgröße?

Betrachtet man die h,x-Diagramme in den Bildern 1 und 2, dann fällt auf, dass die t-Linien nicht horizontal verlaufen. Will man also Zustandswerte in einem Diagramm darstellen, dann kann der t-Wert also nicht als Ordinate (y-Achse) verwendet werden. Zur Darstellung muss also jede x,t-Kombination zunächst in eine x,y-Koordinate umgerechnet werden. Die y-Koordinate kann so gewählt werden, dass t und y für x = 0 identisch sind.

’ Y aus t und x

Function FY_t_x(t#, ByVal x#) As Double

If x < 0 Then x = 0

Ft_x_Y = t * (1 + x * cpd / (cpl * 1000))

End Function

’ t aus x und y

Function Ft_x_Y(x, Y#) As Double

If x < 0 Then x = 0

Ft_x_Y = y / (1 + x * cpd / (cpl * 1000))

End Function

Natürlich kann man die Umrechnung aller anderen Zustandsgrößenkombinationen nach y vollständig implementieren. Da oben aber bereits alle Umrechnungen nach t und x implementiert wurden, ist die Umsetzung nun trivial. Auf eine Beschreibung wird daher verzichtet.

Fazit

Im vorliegenden Artikel werden Berechnungsfunktionen für feuchte Luft dargestellt und erläutert. Es handelt sich um einen vollständig orthogonalen Funktionssatz, der es erlaubt, Feuchte- und Enthalpie-Berechnungen z. B. in MS-Excel durchzuführen. Es können alle Zustandsgrößen des Mollier h,x-Diagrammes ineinander umgerechnet werden. Damit sind vollständige Anlagenberechnungen für klimatechnische Systeme bis hin zu energetischen Berechnungen auf Stundenbasis möglich.

Die dargestellten Berechnungsfunktionen wurden unter Visual-Basic implementiert, eine Übertragung auf andere Programmiersprachen ist allerdings leicht möglich. Fehlerprüfungen und zusätzliche Kommentare wurden zu Gunsten der Übersichtlichkeit aus dem Programmtext entfernt.